自1952年邦德（F•C•Bond）提出第三粉磨学说以来，邦德功指数即作为一种预测和评价物料易磨性的方法迅速在世界范围内得到广泛应用。继欧美许多发达国家先后制定本国的粉磨功指数试验标准方法之后，1976年日本也发布了JIS M4002标准。我国基于邦德方法制定的水泥行业标准于1986年开始实施，至1989年正式颁布执行国家标准（GB9964），迄今应用已十分普遍。各国标准虽然对试验的具体规定有所不同，但都是以邦德方法为基础，其原理并未根本改变，用邦德功指数测定和表征物料易磨性的方法在国际粉体工程界仍具有不可替代的作用。然而，围绕邦德方法展开的讨论却始终没有停止，各国研究者对其复杂的试验过程提出了许多不同的观点或改进方法。这些观点及方法为进一步研究和完善我国水泥原料易磨性试验提供了丰富的参考、借鉴内容。本文集众家之言，简述各种方法的基本过程、应用效果及其评价。

       1 邦德功指数试验的基准方法

       粉磨功指数按邦德裂缝学说即所谓的第三粉碎理论可描述为：磨机所需的粉磨功与物料颗粒的新生裂缝长度成正比，且等于由产品表示的功减去给料所表示的功，即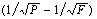：，对于相同形状的颗粒，裂缝长度相当于1/2表面积的平方根，而新生裂缝的长度正比于 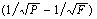。其数学表达式为：

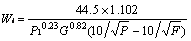
式中：W—磨机输入功，kWh/t；
Wi—粉磨功指数，kWh/t；
 P —80%通过的产品粒度，mm；
F —80%通过的给料粒度，mm。

       按照这一原理，物料在给定的试验条件下经逐个粉磨周期反复粉磨，在第一次粉磨之后的每一周期不断筛出符合于指定粒径P1的成品并补充以等量的新给料，据此计算磨机下一粉磨周期所需的转数，直至达到平衡状态。取最后三个粉磨周期磨机平均每转产生的成品量G（g/r），由下式求得物料的粉磨功指数Wi（kWh/t）。 由式求得的Wi表示物料在Φ2.44m湿法、闭路球磨粉磨条件下所需的单位产量电耗（kWh/t）。对不同于此的生产应用，按邦德提出的磨机有效内径、粉磨工艺（干法与开流粉磨）、入料和产品粒径等一系列修正系数，引入实际生产条件加以修正。修正后的Wi值即为工厂的生产计算值。

       2 围绕邦德方法的讨论

       邦德方法作为各国原料易磨性试验的基础，其理论较之雷廷格（Rittinger）、基克（Kick）的表面积或体积学说所反映的客观性和实用性早已得到公认；其试验方法体现了粉磨过程中的大量变量，并用明确的物理概念定性和定量地将物料易磨性表示为单位产量所需的粉磨功（kWh/t）。但是，邦德方法在操作上存在许多不足，一是需要特制的试验磨机（Φ305mm×305mm）；二是试样处理量大（12~15kg）；三是粉磨周期长（约8~12h），加之大量的试样缩分、筛析和计算工作，使其试验条件近乎苛求、操作过于复杂。因此，各国研究者进行的讨论，其焦点多集中于简化邦德方法的试验过程，提出了实测法、模拟法、对比法、数学估算法以及计算机仿真等下述的各种改进方法。

       2.1 史密斯（Smith）和李（Lee）的方法 该方法认为，邦德试验中的合格成品粒径P1按生产要求已在试验前确定，试验唯一需要得出的就是磨机每转产生的成品量G（g /r）。他们通过8种物料试验发现，不同的P1与G之间为一直线关系，应用这种关系，仅简单试验即可近似地求得最终结果。因此，于1968年提出下式用于粉磨功指数Wi的计算。

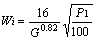
       2.2 卡普尔（Kapur）方法 美国学者卡普尔根据磨矿动力学的线性关系，1970年提出邦德功指数的模拟试验方法。他用原料入磨量M、入磨筛余r、粉磨时间t以及由这些参数所决定的函数Φ等来描述粉磨成品的筛余量R，即R=rMΦt。利用这一表达式，仅用试验的前两个粉磨周期便可完成相当于平衡状态的全过程。在这一方法中，函数Φ按照指数衰减关系，第一粉磨周期的成品筛余量R为：R1=r M1exp（G1t1）；第二粉磨周期为R2=r M1exp（G1t1+ G2 t2）+ rM2exp（G2 t2）。式中M1、M2为各自的新给料量，t1、t2为各自粉磨时间，G1、G2为各自成品量。据此确定的粉磨功指数Wi计算式为：

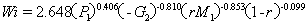
       2.3 卡莱（Karra）的方法 卡莱针对邦德方法中由于入磨物料细粉量较多给筛析增大的难度，提出在第一个粉磨周期之前即筛出过细的部分，直接以粗粒料入磨，使筛分只限于每一粉磨周期的新增量，从而减少筛分量，缩短试验的时间。他于1981年提出计算功指数的统计方程式中，还同时考虑到这样一个事实，即第一粉磨周期的成品被筛出后，循环于以后各周期的物料大多由较硬颗粒组成，因此，其粉磨效率实际偏低，应在试验中有所区别。其采用多次回归方法确定的计算式为：

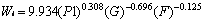
       2.4 N•M•M的数学估算法 荷兰N•M•Magdalinovie研究了邦德方法中P、G和Wi三值之间的变化关系，提出利用已知某一P1筛的试验结果，求得其它细度的功指数计算方法。他认为：同P1相对应的各成品量G呈一直线分布，G正比于P1值的平方根，表示为G =K1 ；K1=G/ 。而P1与80%通过的成品粒径P则为线性关系，即P1=K2•P；K2=P1/P。用最小二乘法处理式中的可磨性系数K1和比例系数K2，即可得到不同细度的G和P，并直接用于粉磨功指数的计算而无须进行专门试验。例如：已知一种原料在入磨粒径F=2200mm，要求产品粒径P1=74mm的条件下，通过邦德试验得到产品80%通过粒径P =50mm、成品量G=1.05g/r、试验功指数Wi=14.55kWh/t。求该原料P=104mm的粉磨功指数Wi为： 即：P=104mm所用的筛孔直径P1=1.48P = 1.48×104 =154mm，试验磨每转产生的成品量 g/r。将P1和G引入下式从而得到该细度的粉磨功指数计算值Wi（kWh/t）。

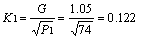
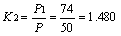
       即：P =104mm所用的筛孔直径P1=1.48P= 1.48×104 = 154mm，试验磨每转产生的成品量g/r。将P1和G引入下式从而得到该细度的粉磨功指数计算值Wi（kWh/t）。

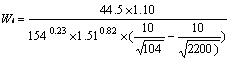
    =14.27（kWh/t）

       2.5 天津水泥工业设计研究院的方法 我国天津院在邦德试验的基础上于1978年提出的改进方法，旨在缩小试验与工业值间的差距和舍弃其繁琐的修正过程。认为邦德方法设定的选粉效率100%，与国内工业生产中的选粉效率偏高，应按实际生产水平设定为75%。这样，邦德方法达到平衡状态的成品量G=Q /（2.5+1），在该方法中即改为： 式中Q为入磨物料量。所得G连续三磨达到平衡状态的平均值即作为物料的易磨性（g/r）直接用于生产。这一方法在过去的较长时间内，一直用于国内水泥生料易磨性的测定。

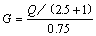
       2.6 合肥水泥研究设计院的修正方法 在邦德方法中，包括功指数Wi的试验和修正两个过程。合肥院提出的方法即是对其修正过程中一些系数的取值进行了改进。认为邦德修正方法一是对磨机的修正只限于有效内径D，即C1=（2.44/D）0.2 ，而试验和修正过程均未涉及磨机长度，这与产量随磨机长度增大而提高的实际情况不相符；二是由成品细度筛余决定的开流粉磨修正系数取值偏高。其成品筛余为5%和8%的开流磨产量，按邦德系数修正，两者分别低于闭路磨46%和57%，而我国的普遍生产水平仅为30%左右。因此，在这一方法中，功指数Wi的应用对标准工业磨机的长度作了界定，其开流粉磨修正系数则取值为1.30。经各项修正系数C1~C6修正后的粉磨功指数，即由试验值Wi转化为相当于实际生产的工业值Ws。表示为：

Wi•C1~C6 = Ws

       该方法同时认为，对功指数Wi的修正，是邦德方法的组成部分，应在标准中予以体现和规范，我国现行标准在此方面目前尚存在不足。

       2.7 贝雷（Berry）、布鲁斯(Bruce)的方法 贝雷和布鲁斯等人1966年提出的对比法类似于传统的相对易磨性试验方法。它采用一种已知邦德功指数Wi的物料作为标准试样，等量（2kg）与其他待测物料分别入磨粉磨至一定时间，由于两种物料的粉磨条件完全相同，所以，根据粒度P和F的变化来求得邦德功指数Wi，即：

标准样       　  　　　试验样

       2.8 霍斯特（Horst）等人的方法 霍斯特和巴萨利尔（Bassarear）1976年提出的方法与之相似。他虽然也按上式对比计算邦德功指数，但力求反映物料的硬度关系和试验的重现性。在这一方法中，其粉磨时间不同，粉磨过程被假定为一次方程关系，成品粒径P取决于下式表示的大于任一特定粒径的消失速度：

lnCi = lnCoi– tki

       式中：Ci表示第i级筛累积筛余量；Coi为物料筛余前的Ci值；t为粉磨时间；ki为大于第i级筛粗粒部分的破碎系数。

       2.9 中南工业大学的计算机仿真方法 中南工业大学在解析邦德方法的数学模型并进行二次模型化和计算机程序化的基础上，1983年建立的计算机仿真测试方法可使大量的试验过程通过计算机操作得以完成。其仿真程序用BASIC语言编制，只需输入F、P、磨机转速N、循环负荷C及其控制误差ε和成品量G的控制误差δ以及表示新给料矿物性质的Si和bij等参数，计算机程序即可依据K次粉磨循环（tk）的系统参数同时满足于下列条件来判定试验达到稳定状态，从而结束系统仿真。

│G（tk）- G（tk -1）│≤δ

│C ( tk ) –2.5│≤ε

       此时的G即为试验磨平均每转产生的成品量，而F和P则由计算机对入料与产品的粒度分布进行组合插值得到，最后由仿真程序按邦德方法计算出功指数Wi。

       2.10 奎克•切克（Quick Check）的方法 奎克•切克认为，邦德基准试验中，入磨物料80%通过的粒径F在规定范围时，只有成品粒径P1发生变化，产品80%通过的粒径P才得以根本改变。当成品筛筛孔过细时，筛析精度降低，因此P1≤120μm筛析的成品粒径P实际上仅为推测值。如果取其平均筛余值R用于下式计算粉磨功指数Wi，也具同样效果。其计算式为：

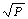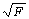式中：R=44.5/P10.23•(10/-10/)-1

       2.11 亚什玛（Yashima）等人的方法 亚什玛等人1970年发表的方法完全不同于邦德基准试验方法，它采用因次分析将邦德功指数Wi与物料的密度ρ（kg/cm3）、脆性指数Bｒ 、抗拉强度S（kg/cm2）、杨氏模数Y1（kg/cm2）、横向变形系数ν1（泊松比）、产品比表面积与圆柱样品的比率Rc和慢速加压下破碎产品比表面积与球形样品的比率Rt等力学性质建立联系，在确定上述7个物理量之后，按下述经验式求得粉磨功指数Wi。此时的功指数试验过程完全改变为上述物理量的检验过程。

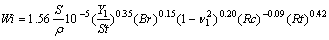
       2.12 阿纳康达（Anaconda）的方法 阿纳康达研究中心注重粉磨设备和物料硬度对粉磨效率的影响，提出一种可用于任一试验磨机的简化方法。这一方法先采用几种已知邦德功指数Wi的物料对选定的试验磨机进行校准，确定出一个适用于该磨机的校准常数A。改变磨机规格或运转参数时，A值应按给定的校准程序或双对数曲线重新确定，以适应磨机结构上的物理和流体特性。在试验过程中，被测物料经破碎（≤10目）、筛析（筛除≤100目的细粉）后，取100目筛上物作为入磨物料，使首次入磨的粒径即相当于邦德试验达到平衡状态时的粒度分布。其入料量也仅用1kg，在加水50%浓度下粉磨10min，最后通过筛析入料粒度F和产品粒度P，按下式求得粉磨功指数Wi。 由于物料在破碎、粉磨过程中的颗粒形成与其硬度有关，在同一粉磨周期内的入料粒度F与产品粒度P的相差程度上能够精确地反映出相对的硬度关系。

      (短吨)

       3 各种方法的比较与评价

       上述各种方法，从形式上大致可分为两种类型，一是单纯为简化操作、缩短试验过程和时间而进行方法的改变，如：模拟对比法、数学估算法等；二是不改变邦德基准方法，只对其某些参数进行改进或程序的优化，如：修正法、计算机仿真等。大多数方法则两者兼备，即：在改变试验参数或方法的同时也简化了操作过程。无论何种方法，虽然其论点分歧较大，但都遵循于邦德粉磨原理，因此，即便其操作过程自成体系，可独立用于物料粉磨功指数的试验，而最终结果则几乎都与邦德基准方法进行误差比较来检验其准确性。按研究者提供的资料和笔者的试验对比，上述方法与邦德功指数存在的误差综合列于表1。

       由表看出，单纯以简化操作或依据参数间的某种线性关系来改变试验方法，其结果必然与邦德方法偏差较大。正如研究者所说，一些参数与粉磨动力学之间的关系不明确，服从于物料的试验条件并不具备邦德方法的普遍适用性等等，都是构成这些方法难于替代邦德试验的主要原因。然而，其中的许多观点及措施，对于完善近五十年来基本不变的邦德方法，拓展改进和创新思路，则无疑具有参考和借鉴价值。各种方法的主要论点及其评价见表2。  

       4 结 语

       上述方法存在的不足，是其不能被广泛应用的主要原因，笔者认为：准确的粉磨功指数应按标准方法通过试验实测获得。邦德功指数及其试验方法在近半个世纪的应用中，有待不断发展、完善和更新，但其焦点并非仅限于试验过程的简化，而应结合我国实际情况注重于对一些偏离国情的参数加以选择和规范；对Wi 的修正应作为试验的组成部分纳入标准规定。合肥水泥研究设计院的修正方法，通过近1000例各厂水泥原料的实测和生产计算，均显示出良好的应用效果。而计算机技术地应用，则体现了试验手段的先进性和发展的必然性，在计算机应用十分普及和技术飞速发展的今天，亟待开发准确、适用的粉磨功指数试验仿真程序，这是简化试验的有效途径。我国应加强这一技术的研究。

       参考资料

       [1]罗 帆•磨机的粉磨参数与物料易磨性• 建材工业技术• 1994.（3）：5.

       [2]冯树祥译•球磨机磨矿能耗的计算•国外非金属矿与宝石•1990.（3）：22.

       [3]高长明•水泥生料的易磨性试验方法及其应用•中国第二届全国破碎与磨碎学术会议论文集•1985：32.